Living organisms are open systems. As such they exchange matter and energy with their surrounding environment.
The vast field of non-equilibrium thermodynamics can help understanding tissue engineered settings both from
an experimental perspective and from a theoretical perspective. An engineered living system still obeys the law of nature.
Non-equilibrium thermodynamics are laws of nature that were unravelled by Prigogine and Glansdorff starting in 1955 but
are still poorly taught in classical curricula or are completely overlooked.
For a closed and isolated system or for the universe as a whole (system + surroundings), the total entropy always increases and
a closed and isolated system inexorably tends to a thermal death. The equilibrium state is the state of such a system where entropy is maximum
and the disorder is maximum.
This is the famous second law of thermodynamics. What happens for open systems departed from equilibrium
(either close to equilibrium or far away from equilibrium)? Open systems are either not isolated (energy flows through the system boundaries)
or not closed (matter is exchanged through the system boundaries).
Prigogine showed that open systems can exhibit spontaneous self-organization by dissipating energy to the surroundings
to compensate for the entropy decrease in the system. Prigogine called the temporal or spatial structures that can arise
dissipative structures.
Sustaining an auto-organised living complex structure or
sustaining oscillations in a system (e.g. heart beats in a living organism) require an open system with constant influx of new reactants and removal of waste products.
A living organism or an engineered living tissue encompasses living cells in a scaffold. These cells interact together and these cells have
a genetic information they comply with. It is a challenge for the scientific community to include the interaction patterns and
knowledge collected from omics data in the non-equilibrium thermodynamical models. How omics data and knowledge theireof will be
incorporated in the in-silico models of engineered tissue in regenerative medicine?
Below, basic materials are provided to remind our fellow community of concepts and methods useful to a proper
non-equilibrium thermodynamical approach of open systems:
- Gibbs chemical potential, De Donder affinity and entropy variation in chemical reactions;
- Entropy production, stability and fluctuations;
- Non-equilibrium thermodynamics;
- Linear regime in non-equilibrium thermodynamics;
- Non-linear regime in far-from-equilibrium thermodynamics;
- Non-equilibrium stationary state;
- Dissipative structures;
- Dissipative structure 1: chemical oscillations (Belousov-Zhabotinsky);
- Dissipative structure 2: Turing structures;
- Dissipative structure 3: Brusselators;
- Non linear dynamics, attractors, chaos, fractals and all that.
Go directly to where you are interested in :
De Donder's Affinity : the driving force of chemical reactions
We are going to define De Donder's extent of a chemical reaction as
\(\xi\), and affinity as \(\mathcal{A} = -\,\sum\limits_{k} \nu_k\,\mu_k\).
\(\mu_k\) is the
Gibbs chemical potential for chemical species \(k\),
\(\nu_k\) the stoechiometric coefficient of chemical species \(k\).
The time derivative of the extent of the reaction is the reaction rate for the chemical reaction:
\( v_k = \frac{d\xi_k}{dt} \).
When De Donder introduced the affinity and the extent of an irreversible chemical reaction inside a system,
he had in mind that the entropy production rate should be a product of a thermodynamical driving
force (affinity) with a thermodynamical flux (chemical reaction rate). This lead to a simple relation
between the entropy production and the chemical reactions.
It is usual to decribe a chemical reaction by the change in the mole number
of reactants and products.
Diffusion is also described in terms of mole number. We start from the Gibbs formula for
the internal energy change:
$$ dU = TdS - pdV + \sum_{k=1}^{n} \mu_k\, dN_k $$
The \(\mu_k\) are the Gibbs chemical potentials and can be written (and empirically defined accordingly as well):
$$ \mu_k = \Big(\frac{\partial U}{\partial N_k}\Big)_{(S, V, N_{j \not= k})} $$
It is paramount to keep distinction between irreversible chemical reactions
inside the system and reversible exchanges with the outside . We therefore split
the change in mole number \(dN_k\) into two terms:
$$ dN_k = d_i N_k \, + \, d_e N_k $$
where \(d_iN_k\) is the change due to irreversible chemical reactions inside the system and
\(d_eN_k\) is the change due to matter exchange between the system and the outside.
In his classical formula, Gibbs considered reversible exchanges of matter and heat and
these are contributing to the first part of the entropy change:
$$ d_e S = \frac{1}{T}\,(dU\,+\,pdV) \, - \, \frac{1}{T}\sum_{k=1}^{n} \mu_k\cdot d_e N_k $$
De Donder wrote that the entropy production \(d_iS\) due to chemical reactions is given by:
$$ d_iS = -\frac{1}{T} \sum_{k=1}^{n} \mu_k\cdot d_iN_k \,\gt 0 $$
In the progress of a chemical (irreversible) reaction, \(d_iS\) is ALWAYS POSITIVE to comply
with the second law of thermodynamics.
As the reaction rates of the chemical reactions determine \(\frac{dN_k}{dt}\) through
\(\frac{d_iN_k}{dt}\), the entropy production rate writes:
$$ \frac{d_iS}{dt} = -\frac{1}{T} \sum_{k=1}^{n} \mu_k\cdot \frac{d_iN_k}{dt} \, \gt 0 $$
Now, let's describe the preceding formula as a product of a chemical driving force (affinity)
with a thermodynamical flux (flux or rate, the chemical reaction rate or temporal variation in the
extent of the reaction).
Consider the following very simple chemical reaction in a closed system,
i.e. \(d_eN_k = 0\) and so \(dN_k = d_iN_k\).
$$ X\,+\,Y \rightleftharpoons 2Z $$
The mole number changes in the components X, Y and Z are \(dN_X, dN_Y, dN_Z\) and we have:
$$ \frac{dN_X}{-1} = \frac{dN_Y}{-1} = \frac{dN_Z}{2} \equiv d\xi $$
where \(d\xi\) is the change in the extent \(\xi\) of the reaction. This helps writing
both the total change in entropy and the entropy change due to the chemical reaction:
\begin{eqnarray}
dS & = & \frac{1}{T}(dU+pdV)\,-\,\frac{1}{T}(\mu_X + \mu_Y - 2\mu_Z)\,d\xi \\
d_iS & = & -\frac{1}{T}(\mu_X + \mu_Y - 2\mu_Z)\,d\xi
\end{eqnarray}
Defining affinity as a new state variable:
$$ \mathcal{A} = -\,\sum_{k} \nu_k\,\mu_k $$
The stoechiometrical coefficients \(\nu_k\) are positive numbers for reactants and negative for products.
Affinity is the driving force for the chemical reaction. If the affinity is not equal to zero, it means
the system is not at thermodynamical equilibrium. In terms of affinity, the entropy increase rate writes:
$$ \frac{d_iS}{dt} = \underbrace{\frac{\mathcal{A}}{T}}_{force}\,\cdot\,\underbrace{\frac{d\xi}{dt}}_{flux} \gt 0$$
and the entropy production due to a chemical reaction is indeed the product of a thermodynamical driving
force (affinity divided by temperature) with the thermodynamical flux, the reaction rate \(\frac{d\xi}{dt}\) here.
When equilibrium is reached, the affinity vanishes and the entropy production vanishes as well.
If there are several chemical reactions proceeding simultaneously in a system
(each reaction is referred to by index \(j \in [1,\cdots,\, n]\)):
$$ \frac{d_iS}{dt} = \sum_j\,\frac{\mathcal{A}_j}{T}\,\frac{d\xi_j}{dt} \ge 0 $$
The above derivation of the entropy production for (irreversible) chemical reactions is formally
analogous to the entropy production when heat is spontaneously and irreversibly transferred from a
hot body (at \(T_1\)) to a cooler body (at \(T_2\)) with \(T_1\,\gt\, T_2\):
$$ d_iS = -\frac{dQ}{T_1} + \frac{dQ}{T_2} = dQ\big(\frac{1}{T_2}-\frac{1}{T_1}\big) \gt 0$$
So here, the driving force is proportional to the temperature difference and the flux is the heat
transfer rate.
$$ \frac{d_iS}{dt} = \big(\underbrace{\frac{1}{T_2}-\frac{1}{T_1}}_{force}\big) \,\cdot\,\underbrace{\frac{dQ}{dt}}_{flux}$$
Incorporating the Fourier law of heat transfer, i.e \(J_Q\equiv dQ/dt = \alpha(T_1-T_2)\) , \(\alpha\) being the thermal
conductivity, into the previous equation, we have:
$$ \frac{d_iS}{dt} = \big(\frac{1}{T_2}-\frac{1}{T_1}\big) \,\cdot\,\alpha(T_1-T_2)$$
$$ \frac{d_iS}{dt} = \big(\frac{T_1}{T_2\,T_1}-\frac{T_2}{T_1\,T_2}\big) \,\cdot\,\alpha(T_1-T_2)$$
$$ \frac{d_iS}{dt} = \frac{\alpha\,(T_1-T_2)^2}{T_1\,T_2} \,\ge 0 $$
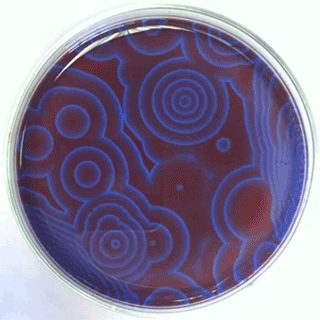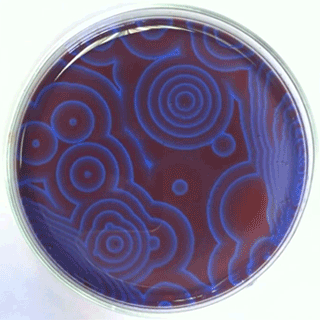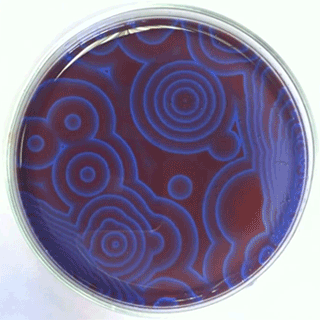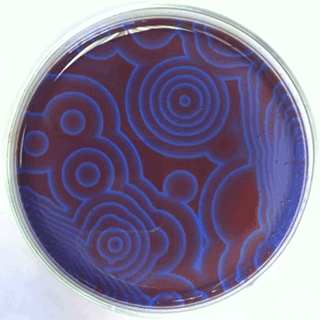
The Belousov-Zhabotinsky oscillating chemical reactions
This page is under construction at the moment...
Chemical waves propagating in a Petri dish...